Knowledge
Tools

Double-click on any word that you do not understand in the text to get its meaning from Cambridge Online Dictionaries. To see the Greek translation of the word, select the option "Greek" and then double-click on the word again. To return to the Cambridge Online Dictionaries select the option "English".
Select Greek translation or English meaning.

Pythagoras Theorem

The Pythagoras Theorem allows us to find the length of the third side on a right angle triangle if we know the other two lengths.

Don’t forget:

It only works on right angled triangles.

You need to know at least two other lengths.

The formal definition is: In a right angled triangle the sum of the square of the hypotenuse is equal to the sum of the squares of the other two sides.

Algebraically a² + b² = c²

('a' squared plus 'b' squared equals 'c' squared)

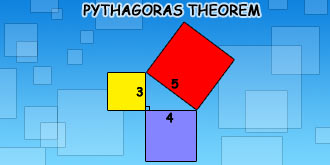
c is always the hypotenuse.

Therefore 3² + 4² = 5^{2

(three squared plus four squared equals five squared)}

Which goes to 9 + 16 = 25

This can be used to find the length of an unknown side

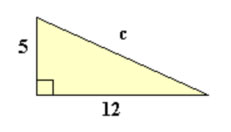
right angled triangle

a² + b² = c²

5² + 12² = c²

25 + 144 = 169

c² = 169

c = √169 (square root of 169)

c = 13

Check that you understand what these words mean in this document
Right angled triangle: the geometrical shape of three sides whose one angle is 90 degrees.
Hypotenuse: the side opposite the right angle.

For further information visit:
Proof of Pythagoras Theorem