Το πυθαγόρειο θεώρημα είναι ένα από τα πιο ελκυστικά και χρήσιμα θεωρήματα της γεωμετρίας.
Παρόλο που το θεώρημα ήταν εμπειρικά γνωστό στους αρχαίους Βαβυλώνιους, φαίνεται πιθανό ότι ο Πυθαγόρας έδωσε την πρώτη γενική απόδειξη του θεωρήματος.
…………
Το πυθαγόρειο θεώρημα έγινε γνωστό σε όλο σχεδόν τον κόσμο, τόσο στη Ευρώπη όσο και στην Ασία. Παρακάτω βλέπουμε ένα ελληνικό κείμενο του θεωρήματος καθώς και πέντε μεταφράσεις του σε διάφορες γλώσσες.

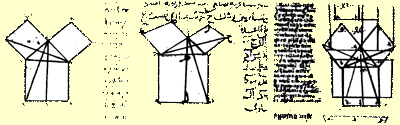Ελληνικό περί το 800 Αραβικό περί το 1250 Λατινικό,1120

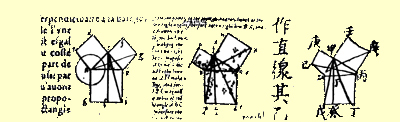Γαλλικό,1564 Αγγλικό, 1570 Κινέζικο, 1607

Ακόμη, κανένα άλλο θεώρημα στα μαθηματικά δεν αποδείχτηκε με τόσους πολλούς τρόπους. Η E.S. Loomis συνέλεξε και ταξινόμησε πάνω από 370 αποδείξεις.
Γύρω στο 1150, ο Ινδός μαθηματικός και αστρονόμος Bhaskara έδωσε μια απόδειξη που περιγράφεται στα παρακάτω σχήματα

Το τετράγωνο της υποτείνουσας ενός ορθογωνίου τριγώνου το χώρισε σε 4 ορθογώνια τρίγωνα ίσα με το αρχικό ορθογώνιο τρίγωνο, και σε ένα τετράγωνο που η πλευρά του είναι ίση με τη διαφορά των καθέτων πλευρών του ορθογωνίου τριγώνου (σχ. 1(α)). Στη συνέχεια τα τοποθέτησε όπως δείχνει το σχήμα 1(β). Είναι χαρακτηριστικό ότι η μόνη λέξη που έγραψε ο Bhaskara στην απόδειξη ήταν «κοίταξε», προτρέποντας μας να παρατηρήσουμε το σχήμα και να δούμε την απόδειξη!
Το 1873 ο Η. Pertgal έδωσε μια απόδειξη που περιγράφεται από το παρακάτω σχήμα 2.

(Α. Αλιμπινίσης, Σ. Γρηγοριάδης, Ε. Ευσταθόπουλος, Ν. Κλαουδάτος, Σ. Παπασταυρίδης, Α. Σβέρκος, Μαθηματικά Β΄Γυμνασίου, ΟΕΔΒ 1988, σελ.102-103)